Staggered grids

Staggered grids are a key component of the marker-and-cell (MAC) method [Harlow and Welch 1965]. They sample the velocity components not at the cell centers but in staggered form at the corresponding face centers. Their main advantage is that the divergence of a cell can be computed exactly.

Φ_Flow only stores valid velocity values in memory. This may require non-uniform tensors for the values since the numbers of horizontal and vertical faces are generally not equal. Depending on the boundary conditions, the outer-most values may also be redundant and, thus, not stored.

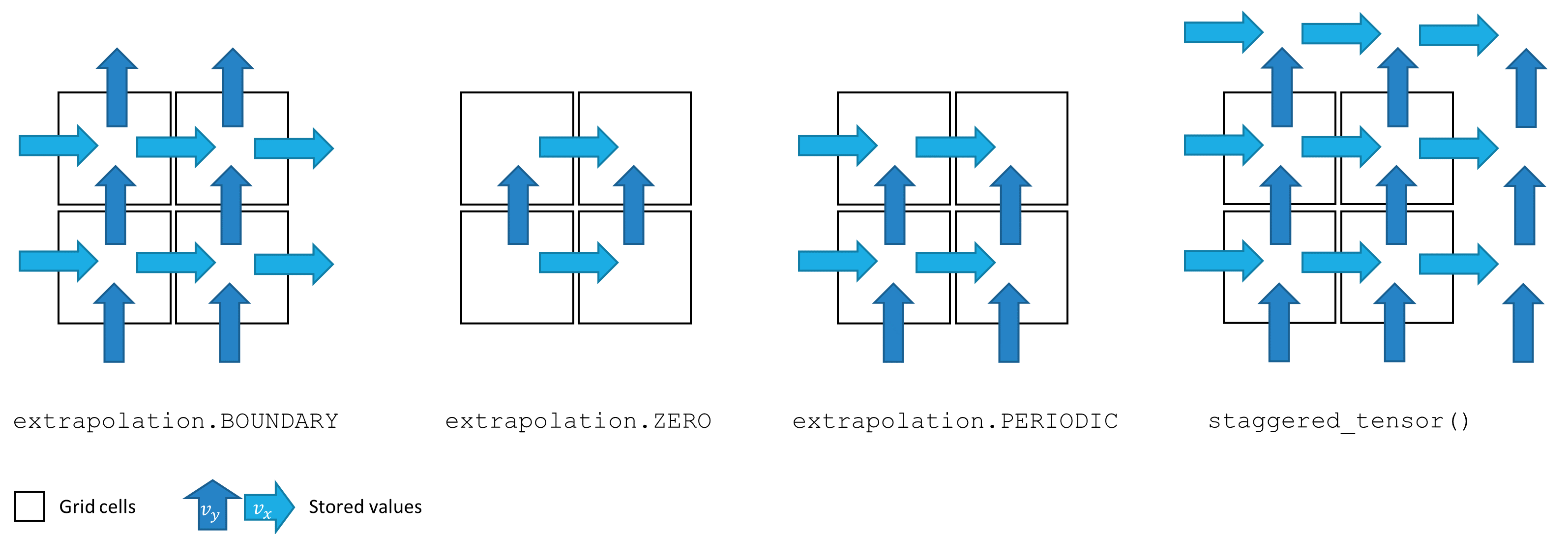
Φ_Flow represents staggered grids as instances of StaggeredGrid. They have the same properties as CenteredGrid but the values field may reference a non-uniform tensor to reflect the varying number of x, y and z sample points.

# !pip install --quiet phiflow
from phi.flow import *

grid = StaggeredGrid(0, extrapolation.BOUNDARY, x=10, y=10)
grid.values

(xˢ=(x=11, y=10), yˢ=(x=10, y=11), vectorᶜ=x,y) float32 const 0.0

Here, each component of the values tensor has one more sample point in the direction it is facing. If the extrapolation was extrapolation.ZERO, it would be one less (see above image).

Creating Staggered Grids

The StaggeredGrid constructor supports two modes:

• Direct construction StaggeredGrid(values: Tensor, extrapolation, bounds). All required fields are passed as arguments and stored as-is. The values tensor must have the correct shape considering the extrapolation.
• Construction by resampling StaggeredGrid(values: Any, extrapolation, bounds, resolution, **resolution). When specifying the resolution as a Shape or via keyword arguments, non-Tensor values can be passed for values, such as geometries, other fields, constants or functions (see the documentation).

Examples:

domain = dict(x=10, y=10, bounds=Box(x=1, y=1), extrapolation=extrapolation.ZERO)

grid = StaggeredGrid((1, -1), **domain)  # from constant vector
grid = StaggeredGrid(Noise(), **domain)  # sample analytic field
grid = StaggeredGrid(grid, **domain)  # resample existing field
grid = StaggeredGrid(lambda x: math.exp(-x), **domain)  # function value(location)
grid = StaggeredGrid(Sphere([0, 0], radius=1), **domain)  # no anti-aliasing
grid = StaggeredGrid(SoftGeometryMask(Sphere([0, 0], radius=1)), **domain)  # with anti-aliasing

Staggered grids can also be created from other fields using field.at() or @ by passing an existing StaggeredGrid.

Some field functions also return StaggeredGrids:

• spatial_gradient() with type=StaggeredGrid
• stagger()

Values Tensor

For non-periodic staggered grids, the values tensor is non-uniform to reflect the different number of sample points for each component.

Functions to get a uniform tensor:

• at_centers() interpolates the staggered values to the cell centers and returns a CenteredGrid
• staggered_tensor() pads the internal tensor to an invariant shape with n+1 entries along all dimensions.

Slicing

Like tensors, grids can be sliced using the standard syntax. When selecting a vector component, such as x or y, the result is represented as a CenteredGrid with shifted locations.

grid.vector['x']  # select component

CenteredGrid[(xˢ=9, yˢ=10), size=(x=0.8999999761581421, y=1.0), extrapolation=0]

Grids do not support slicing along spatial dimensions because the result would be ambiguous with StaggeredGrids. Instead, slice the values directly.

grid.values.x[3:4]  # spatial slice

(xˢ=1, yˢ=(x=10, y=9), vectorᶜ=x,y) float32  0.946 ± 0.067 (3e-01...1e+00)

grid.values.x[0]  # spatial slice

(yˢ=(x=10, y=9), vectorᶜ=x,y) float32  0.991 ± 0.028 (8e-01...1e+00)

Slicing along batch dimensions has no special effect, this just slices the values.

grid.batch[0]  # batch slice

StaggeredGrid[(xˢ=10, yˢ=10, vectorᶜ=x,y), size=(x=1, y=1), extrapolation=0]

Fields can also be sliced using unstack(). This returns a tuple of all slices along a dimension.